Domain of a function

f is a function from domain X to codomain Y. The smaller oval inside Y is the range of f.

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined. That is, the function provides a unique "output" or "value" for each member of the domain.^[1]

For instance, the domain of cosine is the set of all real numbers, while the domain of the square root consists only of numbers greater than or equal to 0 (ignoring complex numbers in both cases). For a function whose domain is a subset of the real numbers, when the function is represented in an xy Cartesian coordinate system, the domain is represented on the x-axis.

1 Formal definition
2 Domain of a partial function
3 Category theory
4 Real and complex analysis
5 See also
6 References

Formal definition

Given a function f:X→Y, the set X is the domain of f; the set Y is the codomain of f. In the expression f(x), x is the argument and f(x) is the value. One can think of an argument as an input to the function, and the value as the output.

The range of f is the set of all values assumed by f for all possible x's; this is the set 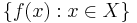$\{ f(x)�: x \in X \}$ .^[2] The range of f can be the same set as the codomain or it can be a proper subset of it. It is in general smaller than the codomain; it is the whole codomain if and only if f is a surjective function.

A well defined function must carry every element of its domain to an element of its codomain. For example, the function f defined by

f(x) = 1/x

has no value for f(0). Thus, the set of all real numbers, 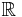$\mathbb{R}$ , cannot be its domain. In cases like this, the function is either defined on 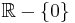$\mathbb{R} - \{0 \}$ or the "gap is plugged" by explicitly defining f(0). If we extend the definition of f to

f(x) = 1/x, for x ≠ 0,

f(0) = 0,

then f is defined for all real numbers, and its domain is 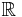$\mathbb{R}$ .

Any function can be restricted to a subset of its domain. The restriction of g : A → B to S, where S ⊆ A, is written g |_S : S → B.

Domain of a partial function

There are two distinct meanings in current mathematical usage for the notion of the domain of a partial function. Most mathematicians, including recursion theorists, use the term "domain of f" for the set of all values x such that f(x) is defined. But some, particularly category theorists, consider the domain of a partial function f : X → Y to be X, irrespective of whether f(x) exists for every x in X.

Category theory

In category theory one deals with morphisms instead of functions. Morphisms are arrows from one object to another. The domain of any morphism is the object from which an arrow starts. In this context, many set theoretic ideas about domains must be abandoned or at least formulated more abstractly. For example, the notion of restricting a morphism to a subset of its domain must be modified. See subobject for more.

Real and complex analysis

In real and complex analysis, a domain is an open connected subset of a real or complex vector space.

In partial differential equations, a domain is an open connected subset of the euclidean space Rⁿ, where the problem is posed, i.e., where the unknown function(s) are defined.

References

↑ Paley, H. Abstract Algebra, Holt, Rinehart and Winston, 1966 (p. 16).
↑ Smith, William K. Inverse Functions, MacMillan, 1966 (p. 8).